Las puertas lógicas conocidas en su forma básica son cuatro, las cuales responden al
Algebra de
Boole.
AND /
OR /
NOT /
XOR.
De las cuatro 3 disponen de dos entradas y una de su única entrada todas tiene una sola salida lógica, estas puestas lógicas se rigen bajo un comportamiento especial el cual está regido por la tabla de la verdad, que es una tabla que resume todas las posiciones posibles de dicha puerta lógica
TIPOS DE PUERTAS LOGICAS
1.- OR (O) Suma Lógica Esta puerta lógica responde a la operación de la suma, la cual es aquella que arroja en su salida un "1" lógico, esto solo si alguna de sus entradas es "1".
.png)
2.-
AND (Y) Producto lógico Responde a la operación de la multiplicación, viene a ser aquella puerta lógica que entrega un "1" lógico en su salida si todas sus entradas tiene "1".
.png)
3.-
NOT (N) Negación Lógica Puerta lógica que entrega el estado lógico contrario al de su entrada.
.png)
4.-
XOR Or Exclusiva Aquella que proporciona un "1", siempre y cuando las entradas sean iguales..png) Otras puertas lógicas
Otras puertas lógicasTanbién tenemos otras puertas lógicas de mucha utilidad en nuestra instrucción.
5.- NAND (Negando Y ) Proporciona en su salida un cero lógico "0" siempre y cuando sus entradas sean "1"
.png)
6.-
NOR (Negando 0) Proporciona en su salida un "1" lógico solo cuando sus entradas tiene un "0".
.png) ALGEBRA DE BOOLE
ALGEBRA DE BOOLE
Se denomina así en honor a George Boole, (2 de noviembre de 1815 a 8 de diciembre de 1864), matemático inglés que fue el primero en definirla como parte de un sistema lógico a mediados del sigo XIX. Específicamente, el álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica proposicional.
Las propiedades del conjunto en el que se han definido las operaciones (+, *, ') son las siguientes:
PROPIEDAD CONMUTATIVA:
De la suma: a+b = b+a
Del producto: a*b = b*a
PROPIEDAD ASOCIATIVA:
De la suma: (a+b)+c = a+(b+c) = a+b+c
Del producto: (a*b)*c = a*(b*c) = a*b*c
LEYES DE IDEMPOTENCIA:
De la suma: a+a = a ; a+a' = 1Del producto: a*a = a ; a*a' = 0
PROPIEDAD DISTRIBUTIVA:
De la suma respecto al producto: a*(b+c) = (a*b) + (a*c)
Del producto respecto a la suma: a + (b*c) = (a+b) * (a+c)
LEYES DE DE MORGAN:
(a+b+c)' = a'*b'*c'(a*b*c)' = a'+b'+c'
LA TABLA DE LA VERDAD
La tabla de la verdad es la manera representativa de una función lógica en la que se indica el valor "0" y "1" para cada valor que toman estas para cada combinación posible que las entradas pueden tomar.Con ella obtenemos su forma canónica de la función lógica, nos es útil para poder simplificar la misma y usar su forma mas conveniente y simple.
Ejemplo.
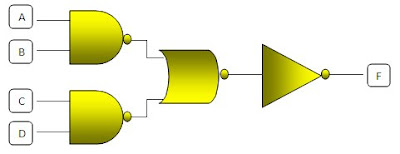.bmp)
.bmp)
Como resultado obtenemos:
F = (A*B*C*D)'
Una puerta
NAND de 4 entradas.
PRINCIPIO DE DUALIDADEste principio nos indica lo
sgte.
A toda ley lógica le corresponde su dual, formada por el intercambio de los operadores lógicos, suma y producto lógicos y los "1" y "0", adicionalmente se cambia cada variable por su valor negado, esta tabla es totalmente necesario para la aplicación de los principios de dualidad.
.bmp) FAMILIAS LOGICAS
FAMILIAS LOGICAS
Todo circuito digital, tiene una cubierta encapsulada, las cuales albergan puertas lógicas de
distinto índole, estos componentes electrónicos tienen un
estándar que posee compatibilidad con muchos fabricantes, de tal manera que sus características sean comunes y compatibles, por ello los componentes lógicos digitales se engloban en dos grandes familias lógicas:
TTL : los cuales proporcionan una gran velocidad de funcionamiento.
CMOS : Los cuales están diseñados para realizar un mínimo de consumo de energía.En la actualidad hay otras familias estandarizadas en cierta características, como por ejemplo la ECL , que pretendía brindar las características de velocidad y bajo consumo de las TTL y CMOS.
.bmp) (*) O lo que permita el tiempo de propagación admisible
(*) O lo que permita el tiempo de propagación admisible
Dentro de la familia TTL encontramos las siguiente sub-familias:
L: Low power = dsipación de potencia muy baja
LS: Low power Schottky = disipación y tiempo de propagación pequeño.
S: Schottky = disipación normal y tiempo de propagación pequeño.
AS: Advanced Schottky = disipación normal y tiempo de propagación extremadamente pequeño.
TENSIÓN DE ALIMENTACIÓN
CMOS: 5 a 15 V (dependiendo de la tensión tendremos un tiempo de propagación).
TTL: 5 V.
Todo componente electrónico es un componente cuyo funcionamiento no es ideal, así también las puertas lógicas reaccionan de la misma manera, por ello están dispuestas de ciertos parámetros, ello por la tecnología utilizada para su fabricación. Las Familias TTL enplean transistores bipolares en su estructura interna, por ello son dispositivos de alto consumo de energia, las Familias CMOS emplean en su fabricación transistors tipo MOS, por ello su bajo consumo de energía.
Entre los parámetros especificados en las puertas lógicas tenemos :
Amplitud lógica Ya que las puertas lógicas de la misma familia no presentan las mismas características, se consideran los valores extremos de manera ideal.
AL máx: VH máximo - VL mínimo
AL mín: VH mínimo - VL máximo
Margen cero Es el rango de tensiones en las entradas que son consideradas como cero lógico.
VIL máx: tensión máx. admisible como cero lógico.
VIL mín: tensión mín. admisible como cero lógico.
Margen uno Es el rango de tensiones en las entradas de una puerta lógica que son consideradas como un "1" lógico.
VIH máx: tensión máx., admisible como uno lógico.
VIH mín: tensión mín., admisible como uno lógico.
Límite de Trasición Margen en el cual la tensión de una puerta lógica puede ser tomada como "1" o como "0" , no es recomendable utilizar este margen ya que tendríamos calculos inadecuados.
Ruido El parámetro con el que más nos encontraremos y que ocacionan que el circuito no funcione correctamente, puede presentarse ruido propio proveniente del mismo circuito, o externo proveniente de causas externas a circuito.
VMH ( margen de ruido a nivel alto) = VOH mín - VIH mín
VML (margen de ruido a nivel bajo) = VIL máx - VOL máx
Fan Out Es el parámetro que nos especifica el máximo número de puertas lógicas a excitar en sus entradas sin evadir los standares de fabricación.
FAN OUT = IOL máx / IIL máx
IOL e IIL , Intensidades de salida y entrada mínimas de puerta.
Frecuencia máx. de uso Esta definida por :
Fmáx = 1 / (4 * &)
& = Tiempo de propagación
Potencia disipada Es la potencia promedio que el dispositivo puede consumir.

.bmp) g .- En nuestro circuito se introduce la combinación para cada casilla, obteniendo una casilla para cada caso, cuando la salida del circuito es un "0" , en la correspondiente casilla se escribe un "0" , mientras que si enm la salida sale un "1" , se anotará un "1" en la correspondiente casilla, con ello el procedimiento para completar las casillas ha terminado, hasta este punto la solución es objetiva, dependiente de las leyes establecidas. Salida = C negada.
g .- En nuestro circuito se introduce la combinación para cada casilla, obteniendo una casilla para cada caso, cuando la salida del circuito es un "0" , en la correspondiente casilla se escribe un "0" , mientras que si enm la salida sale un "1" , se anotará un "1" en la correspondiente casilla, con ello el procedimiento para completar las casillas ha terminado, hasta este punto la solución es objetiva, dependiente de las leyes establecidas. Salida = C negada..bmp)
.bmp)
.bmp)
.bmp)
.bmp)

.png) 2.-
2.- .png) 3.-
3.- .png) 4.-
4.- .png) Otras puertas lógicas
Otras puertas lógicas.png) 6.-
6.- .png)
.bmp)
.bmp) Como resultado obtenemos:
Como resultado obtenemos:.bmp)
.bmp) (*) O lo que permita el tiempo de propagación admisible
(*) O lo que permita el tiempo de propagación admisible